The fractions class
I was teaching a small group of children in a private school – a sort of enrichment class for students in grade 4 who, according to their teachers, were “fast learners”. The mandate given to me was to prepare them for an inter-school Maths competition. I was briefed by their teachers who gave me question sets from previous years’ competitions and practice worksheets.
Even with this “fast learner” group, there were differences, and stark between the two of them – we’ll call them C and X. C was a teachers’ favourite – very diligent and listening to instructions in class, getting full marks on tests, submitting homework on time. X, on the other hand, was good at Maths, but very inconsistent in his work, prone to making “silly mistakes” and very often caught daydreaming in class.
Initially, I stuck to the script, following the guidance of more experienced teachers and sharing worksheets, which were the typical drill and practice. Fractions were a challenging topic, and the worksheets had many questions like these -
While I wondered at the ridiculousness of doing these sums (adding mixed fractions with different denominators, and that too prime numbers!), I followed my mandate. Some children, like C, could do such sums but were doing it mechanically and still struggling with the basics. So, I reworked the worksheets, scaffolded them, and linked them to activities to explain the concepts better.
But it was still very routine. It was more engaging than before, but like the children, I too became bored. Mostly, I was concerned about X, who was not enjoying at all and his work started declining.
Let’s play
We had some geometrical shapes/pattern blocks in the room, used more with children in pre-K or grades 1-2.
One day, I decided "Let's play". I kept the shapes in the middle of the class, and we started playing with them – making different figures freestyle, balancing them on each other, exploring how they fit together and tesselate. One of the explorations led to exploring how the shapes fit on top of each other. E.g. how many triangles would fit in the parallelogram? Which combinations of shapes would make a hexagon? The students came up with the usual (using 6 triangles) and the not-so-usual (combining a triangle, parallelogram, and trapezium).
After we had explored different combinations, we started with simple questions like these -
While C was uncomfortable with this new approach and reluctant to play with no tangible output, X enjoyed it. Whenever X got stuck, he returned to his shapes and figured it out – even for more difficult questions.
I was also amazed at how students started reasoning, later without the shapes, and articulating their solutions in different ways. In this question below, one student explained it using the logic of 2 parallelograms making a whole, so 1 parallelogram had to be half.
One size does not fit all – the same applies to play
Now, did X start doing the mixed fraction sums quicker than C? No, C was faster at calculating and remained faster. Did X at least attempt the mixed fraction sums? Yes, while he was still not excited about doing those sums, he would attempt to finish. He gained more confidence, shared his thinking, and even offered to help C!
One day, C’s mother met me before class one day. “Where can I get more worksheets like these? I teach him at home, and I have not seen these questions before. If I know where to get them, I will make him practice.” I shared our approach and showed her the manipulatives; unfortunately, she was not convinced and insisted on more practice worksheets for these new question types.
The class moved to solving more conventional textbook questions too, but always trying to explore different ways of solving them.
What did I learn from this experience?
Questions/problems given to students can lead to more playful explorations. Moving from mixed fractions sums to ones with pattern blocks led to a deeper understanding of fractions, and also to students talking about angles, symmetry, tessellation, etc.
Teachers need to have more agency, and we need to have systems that promote standards, not necessarily standardized lesson plans or worksheets. If I were not given the flexibility by the school, I could not have explored other ways of engaging students.
Most importantly, for playful learning to happen, we need playful teaching. We need to encourage adults to become more playful. My mindset was the bottleneck. I had to be more flexible, responsive to different students, and more open to getting surprised, amazed, and challenged by new ideas and ways of thinking and making meaning.
In subsequent articles, I will share more experiences with adults, particularly my colleagues and teachers, and how we can encourage more playful mindsets.
Notes
- For more on playfulness, please read this working paper from the Pedagogy of Play.
- For more about the resources used and the inspiration behind the activity, please visit Jodogyan’s website. There are also several websites to explore pattern blocks virtually.






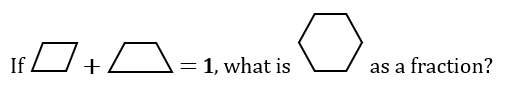
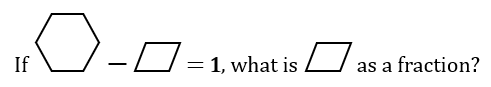
Lovely writing and inspiring approach towards educating children. Much to learn.