Line 1: The curve
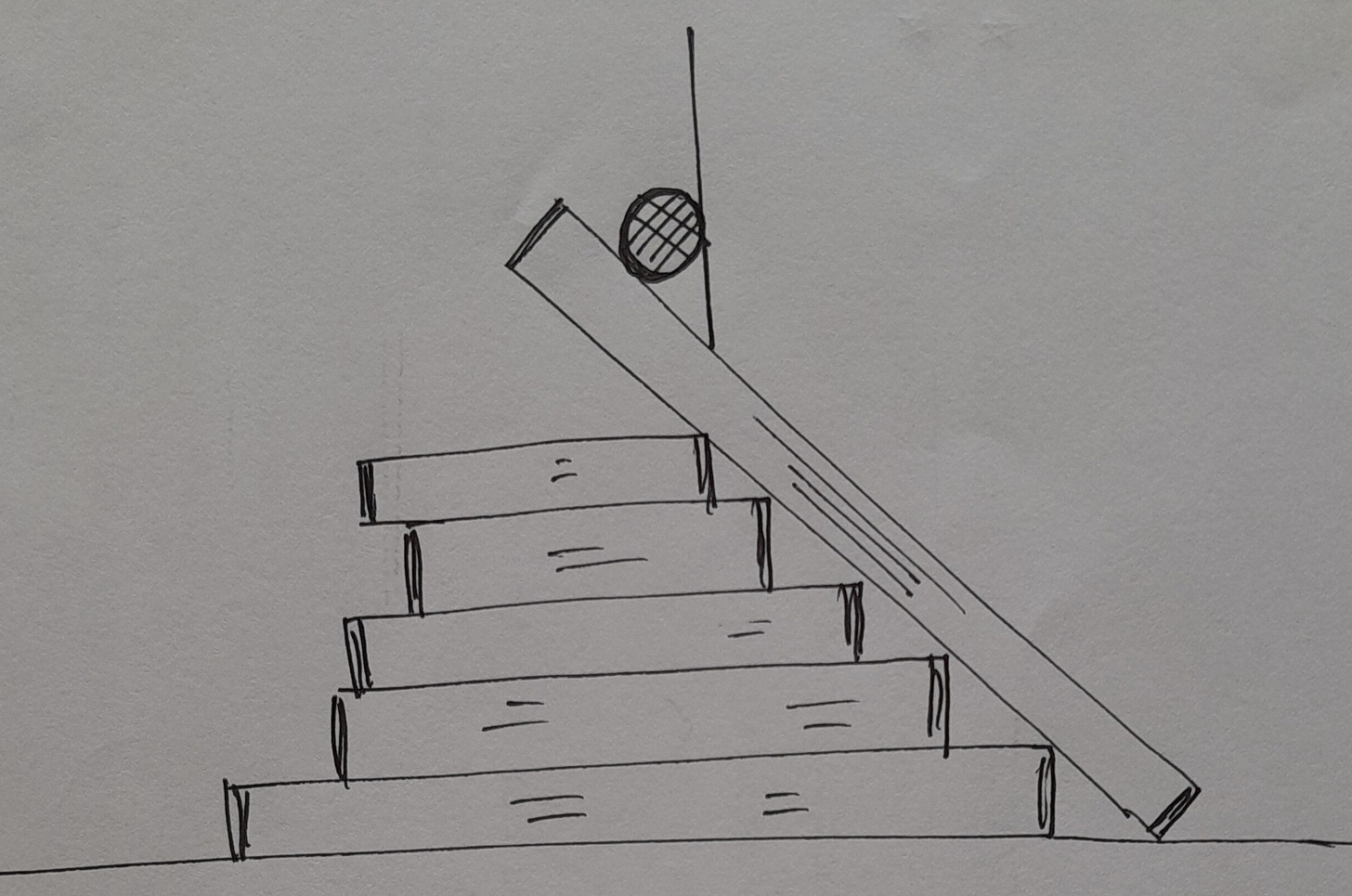
A teacher set up an activity for 5th grade children - an inclined plane with books, and different balls – tennis, table tennis, smiley-face sponge and plastic – for rolling. Children had to guess which ball would roll the furthest and why. The balls would be released from the top of the incline without adding any force. Children would then measure the distance rolled with a scale or tape measure.
So, the children guessed and discussed what could affect the ball’s rollability – its size, weight, whether it was hollow etc.
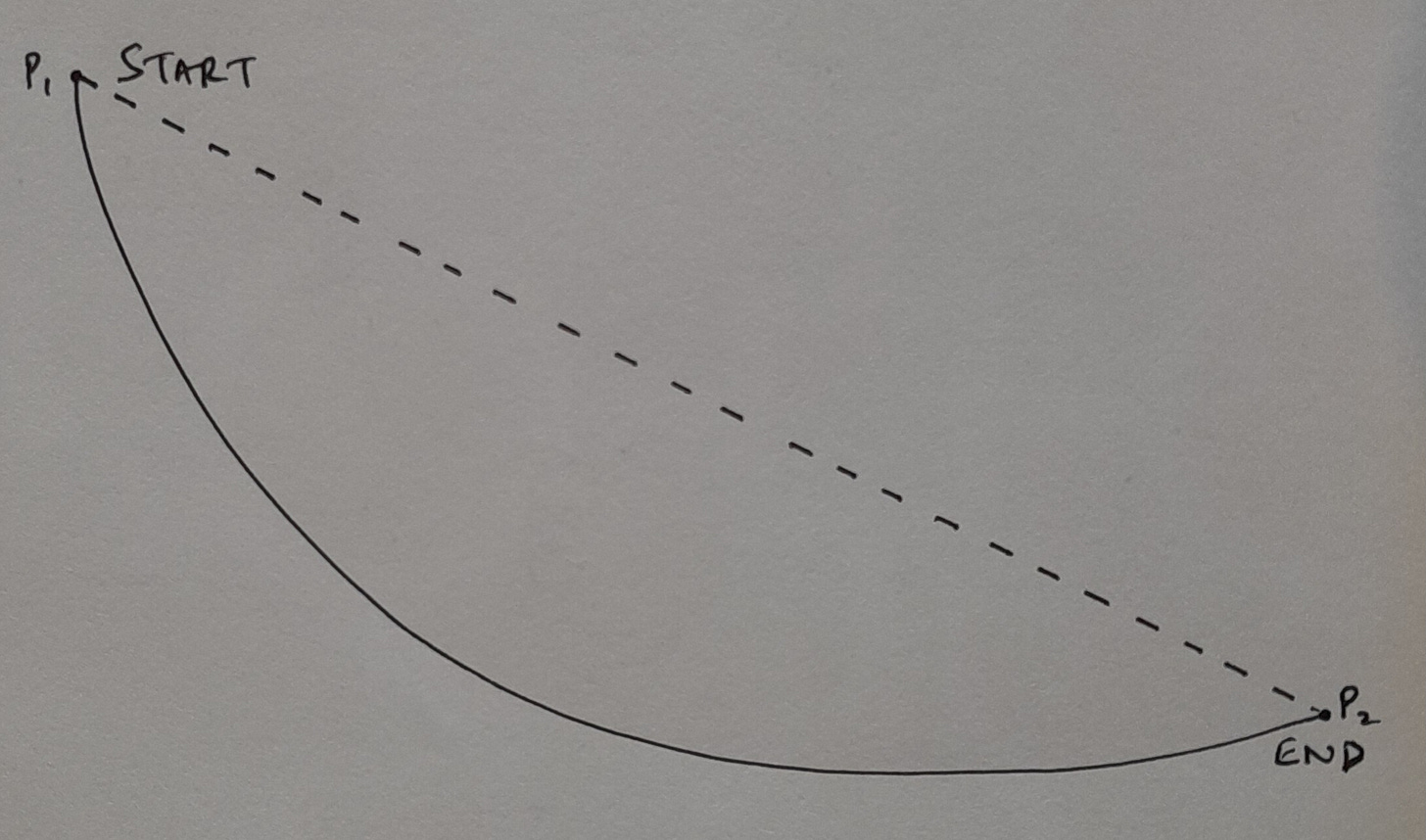
Then, one by one, they let the balls roll. What the teacher had not accounted for was an undiscernible slope of the floor. So, one ball which rolled further also curved a fair bit. Most children measured the distance between the starting and end points as they had done for the other balls.
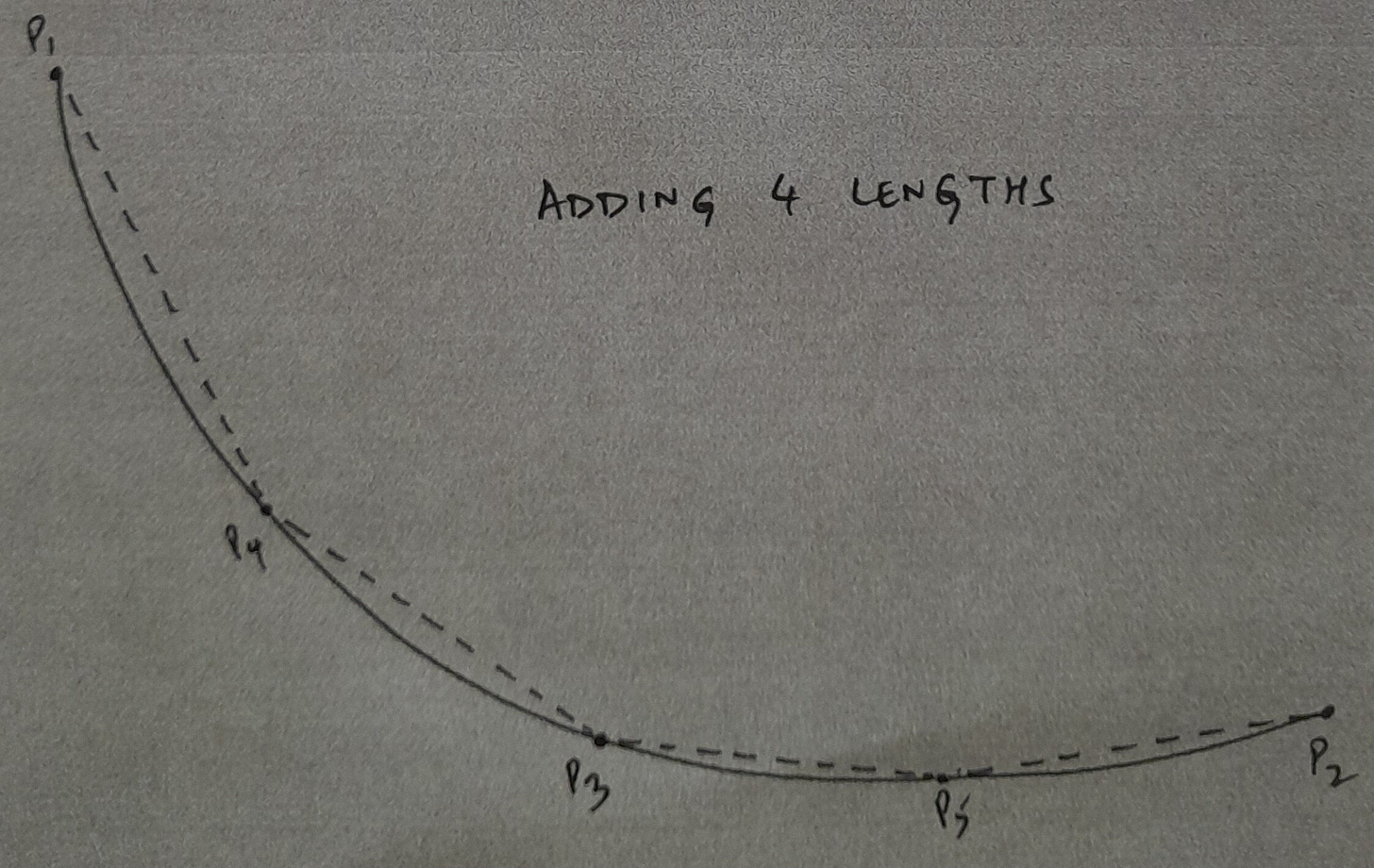
But this ball had visibly curved. “It is longer than this” - one argued. “It has travelled more” – another said. A child who had followed this ball, running behind it all the time to much amusement of others, stood at an in-between point – “It curved till here. So, we can measure from the start to here, and from here to the finish, and add them up.” While doing that, another stood at another in-between point – “It curved from the start to middle too. What if get the middles of these two parts and add up the four lines? This will be even more correct (aur sahi hoga)."
Among all this movement and measurement, a child who was keenly observing this – “We could make many very small lines and add them all up to make a curve.”
Line 2: Sleeping and standing
A visit to a pre-school class with a mixed group of 3-4 year old children. Today, the teacher is teaching the difference between sleeping, standing and slanting lines.
The teacher says - "Khadi rekha banao” (draw a standing line). Children draw on their slates with chalk pieces. One child, M, makes this –
The teacher asks the children to turn their slates towards her and walks around the room to check their work. She sees M’s slate and says “Khadi rekha, khadi rekha!” (Standing line, standing line!).
M looks at his work and turns the slate to show the teacher this –
The teacher is not satisfied and says - "Mitake dobara banao.” (erase and make it again).
M looks at his work again, then at the teacher, ponders, and then erases his work to draw another line.
From missed opportunities to maths talks
Parents and teachers have many such stories of young children, highlighting their creativity, vivid imagination, wit and amazing insights. Children have unique ways of explaining; in ways we may not have understood those concepts ourselves. Even if an activity is simple, conversations can be deep and far exceed what the grade level curriculum expects.
Maths talks is a pedagogical strategy for teaching and learning maths, where children articulate their why and how of solving a problem. The National Curriculum Framework for Foundational Stage (NCFFS) 2022 notes the “need for rich conversation between Teachers and children around mathematical concepts, processes, applications…” and to “provide an opportunity for children to explain their mathematical thinking, reason, justify and listen to other mathematical ideas…”. This is not limited to the early grades; the National Curriculum Framework for School Education (NCFSE) 2023 takes this further in the Middle Stage, i.e. grades 6-8, “Content should provide opportunities for students to ‘talk’ Mathematics.”
Maths talks are a deliberate strategy, planned by teachers. E.g. with a sum like 27+18, the teacher does not stop at the correct answer, and follows up by asking children, “How did you get the answer?”, “Is there another way of solving this?”, “What did you like about <another child’s> method?” However, the teacher had not planned for the ball to curve in the rolling activity; it just provided a great setup for talking maths (and science) with sufficient space for children to explore different ideas playfully. The second story (sleeping and standing) too had no planned maths talk, but was a missed opportunity. Asking the child to share how the sleeping line became a standing line may have triggered more thinking from other children.
We often miss these gems and opportunities. It could be for varied reasons - including teachers feeling pressure to complete the lesson plan with its minute-by-minute breakup.
When things don’t go according to plan, and we see the line moving or the ball rolling away, let's enjoy the moment, open ourselves to new opportunities, listen to children’s insights and learn.
Notes – Please visit YouCubed to learn more about Number Talks
References:
Parrish, Sherry (2010). Number Talks: Helping children build mental math and computational strategies